Skip to main content

Joins Algorithms

在 RDBMS 中，我們常常會依據正規化 (normalization) 的原則將資料放到不同的表格中以避免記錄到重複的資料，因此在查詢時，我們就需要透過 join 來將資料合併。

在這篇筆記中，我們主要會討論兩個 table 執行 join 的不同方法。 一般情況下，我們會希望比較小的 table 作為 outer table，而比較大的 table 作為 inner table。

Join​

在使用 join 運算子時，我們需要注意以下兩個部分 :

  • Output : 連接運算子向查詢計劃樹中的父運算子發出的資料
  • Cost Analysis Criteria : 評估不同的 join algorithms 的成本
Join

Output​

主要有兩種連結方式 :

  • Early Materialization : 將所有的資料都放到新的 tuple 中，這樣之後就不需要在回去表中讀取資料，較適合 row store。
  • Late Materialization : 只複製 join key 跟 record_id，之後再去表中讀取資料，較適合 column store。

Cost Analysis Criteria​

由於資料庫的資料通常無法一次性的讀進記憶體中，因此我們需要透過 join algorithms 來最大化減少硬碟 I/O 的次數，對於 join algorithms 來說，唯一的評論標準就是 I/O 數量。

Nested Loop Join​

這是最基礎、最直觀的 Join 演算法，就像程式語言中的兩層 for 迴圈。

接下來的資料都是基於以下的假設 :

  • 對 RR 跟 SS 兩個 table 做 join
  • RR 有 MM 個 page， mm 個 tuple
  • SS 有 NN 個 page， nn 個 tuple

對於以下的 SQL 來說，表 A 是 outer table，表 B 是 inner table。

SELECT *
FROM A
JOIN B ON A.a1 = B.b1;

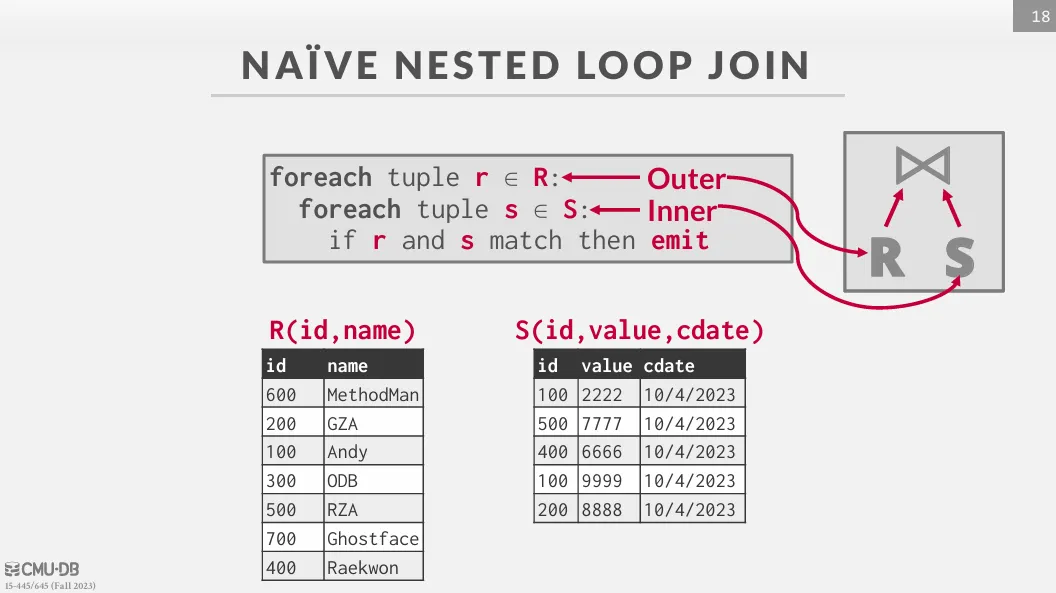
Naive Nested Loop Join​

對於 outer table 的每一個 tuple，都會去 inner table 中掃描全部的 tuple 來進行比對。

Cost 是 M+(m×N)M + (m \times N)

Naive Nested Loop Join

Block Nested Loop Join​

每次取 R 的一個 page 進來，然後對 S 掃描全部的 page。

如果我們有 B 塊 buffer，我們可以將一塊用於 inner table 的掃描緩衝，一塊負責輸出，剩下 B - 2 個則用於 outer table。

Cost 的分析如下 :

  • 單一 buffer : cost 是 M+(M×N)M + (M \times N)
  • 有 B 塊 buffer : cost 則變為 M+⌈MB−2⌉×NM + \lceil \frac{M}{B-2} \rceil \times N
Block Nested Loop Join

Index Nested Loop Join​

前面幾種較慢的原因在於我們需要多次對全表掃描，但若 inner table 在 join attribute 上有 index，我們就可以透過 index 來加速，只需掃描一次即可。

Cost 是 M+m×CM + m \times C，其中 C 是掃描一次 index 的 cost。

Index Nested Loop Join

Sort-Merge Join​

如果兩個 table 都已經依照 join attribute 排好序了，我們就可以透過 sort-merge join 來進行 join。

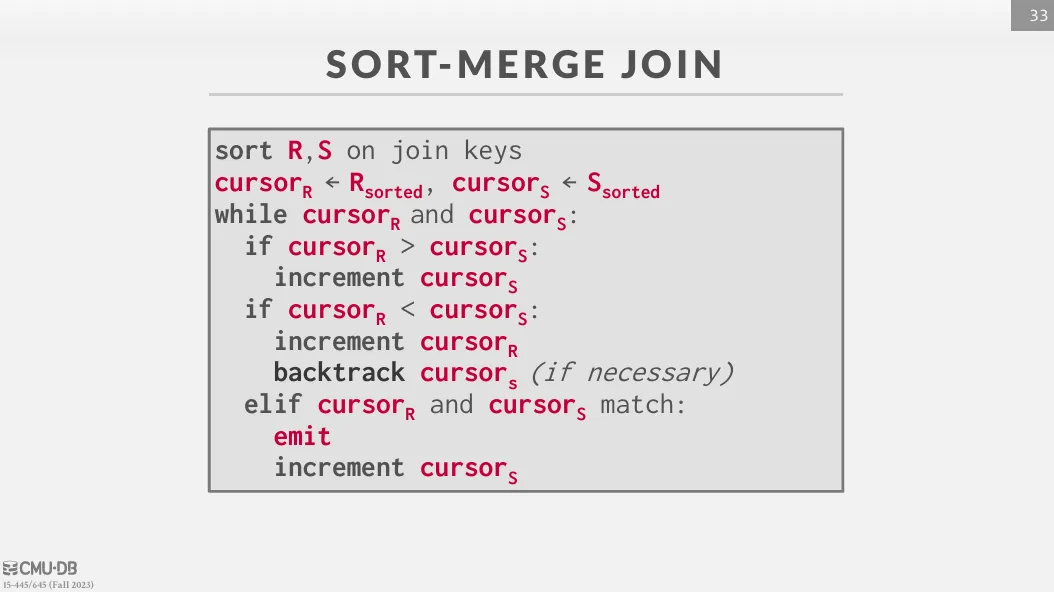
主要分為兩個步驟 :

  • Sort : 將兩個 table 依照 join attribute 排序
  • Merge : 從兩個 table 的端點開始進行掃描，並進行比對，如果遇到重複則需要 backtracking

Cost 的分析如下 :

  • Sort cost (R) : 2M×(1+⌈log⁡B−1⌈MB⌉⌉)2M \times (1 + \lceil \log_{B-1} \lceil\frac{M}{B} \rceil \rceil)
  • Sort cost (S) : 2N×(1+⌈log⁡B−1⌈NB⌉⌉)2N \times (1 + \lceil \log_{B-1} \lceil\frac{N}{B} \rceil \rceil)
  • Merge cost : M+NM + N

最差的情況就是所有的 join attribute 都一樣，此時的 cost 是 M×NM \times N + sort cost。

Sort-Merge Join

Sort merge 主要適用的情境是 :

  • 已經有一個或是兩個 table 已經排序好了
  • SQL 的輸出必須要排序時

Hash Join​

如果有兩個分別在 R 跟 S 的 tuple 有相同的值，則代表他們 hash 之後的值也必定相等，所以我們也可以只針對 hash 之後相同的值進行處理。

Simple Hash Join​

這是最基礎的 hash join 方法，如果 outer table 的 hash table 可以放入 memory 中，則可以使用這個方法。

主要分為兩個階段 :

  • Build : 將 outer table 中的 join attribute 透過 hash function h1 進行 hash，並放入 hash table T 中 (盡量選擇較小的 table 作為 outer table)
  • Probe : 將 inner table 中的 join attribute 透過 hash function h1 得到這個 tuple 在 T 中的位置，並進行比對

其中 T 的 key 是 join attribute，value 則可以是 early materialization 或 late materialization。 在這個方法中，T 有可能沒辦法被放入 memory 中，導致需要進行多次 I/O，如果可以預測 T 的大小，我們也可以使用靜態 hash table。

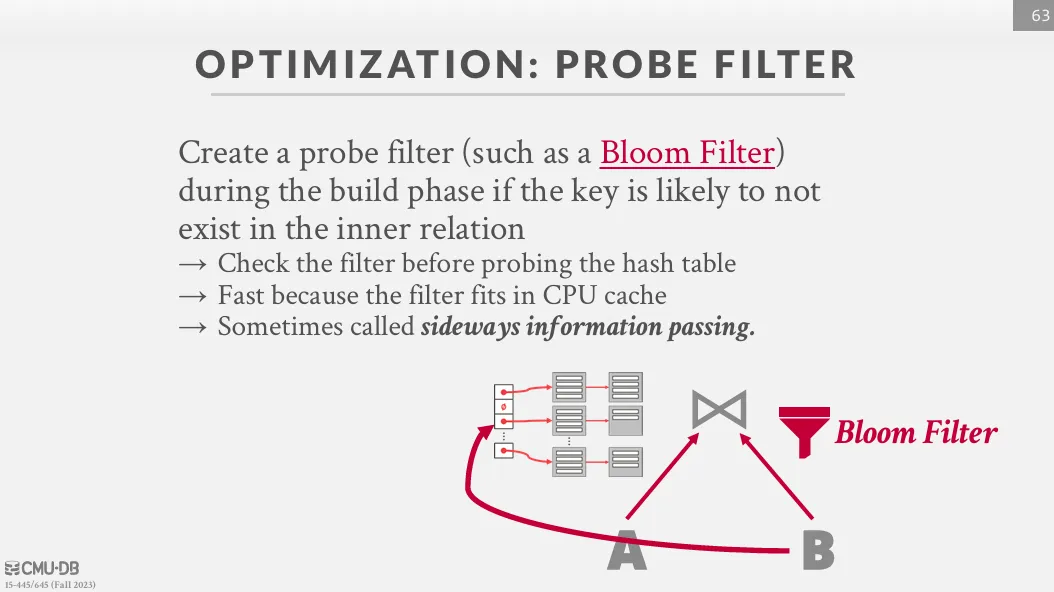
也可以使用 bloom filter 來幫助我們快速找到不在 T 中的 tuple。

Simple Hash Join

Grace Hash Join / Partitioned Hash Join​

如果 hash table 無法放入 memory 中，我們可以使用 Grace Hash Join 來解決這個問題。 這個方法會先將兩個 table 進行 partition，使得每一個 partition 都可以放入 memory 中，然後再對每一組 partition 使用 simple hash join。

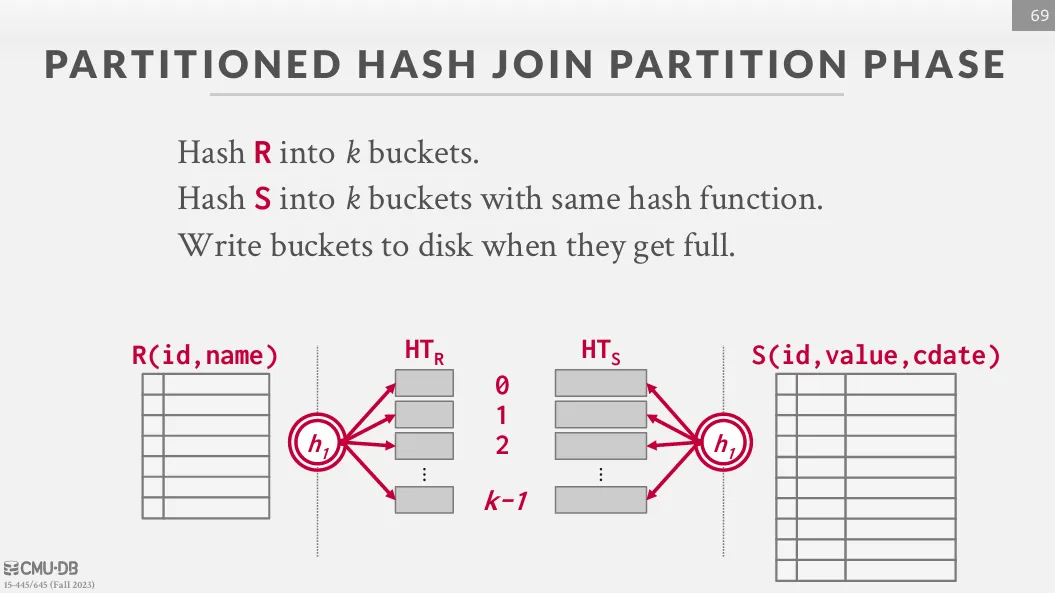
主要分為兩個階段 :

  • Partition : 將兩個 table 使用同樣的 hash function 進行 partition，使有機會配對成功的 tuple 進入同一個 partition 中
  • Probe : 將每一組 partition 中的 tuple 進行 hash join

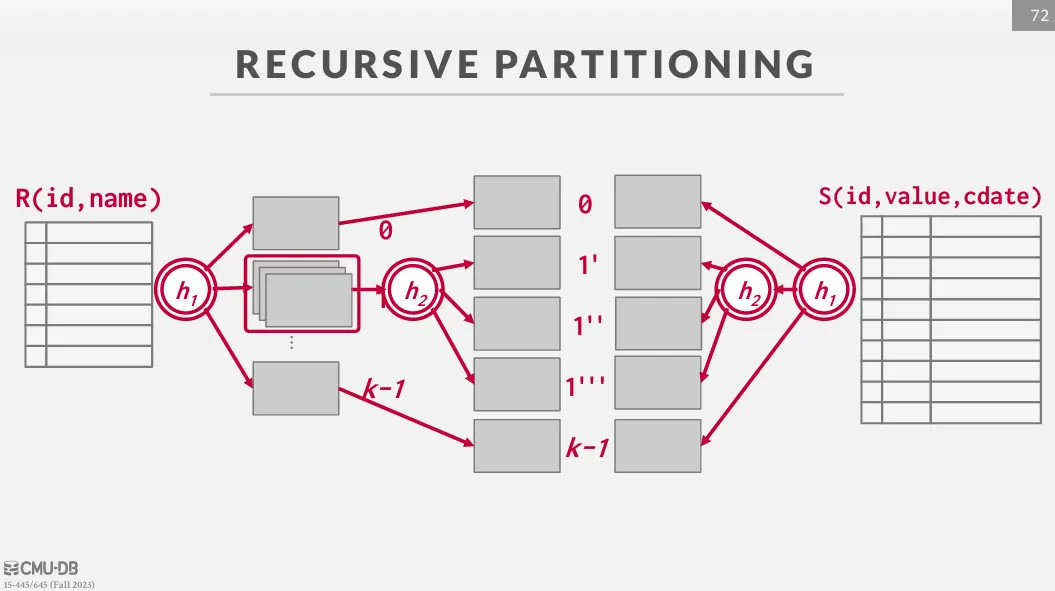
如果一次 partition 後還是無法放入 memory 中，我們可以進行多次 partition (recursive partitioning)，如果單一的 key 有太多的 tuple，可以使用 block nested loop join 來處理。

Cost 的分析如下 :

  • partition cost : 2(M+N)2(M + N) 讀取之後再寫入到 partition 中
  • probe cost : M+NM + N simple hash join 的 cost
  • total : 3(M+N)3(M + N)
Grace Hash Join
Grace Hash Join

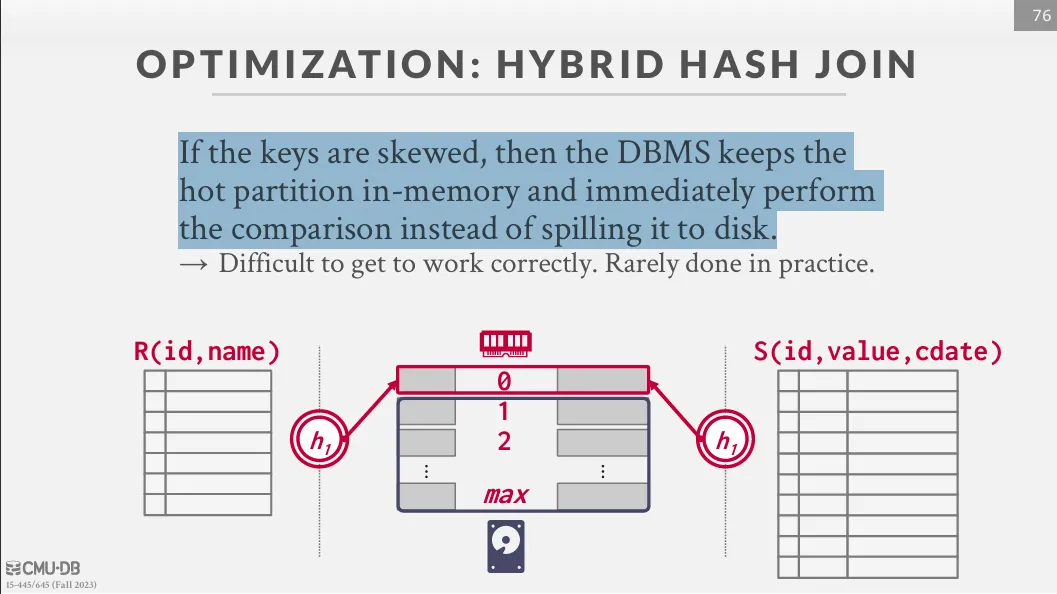
如果有些 key 非常常使用，我們可以將他們放入 memory 中並立即比較，而非溢出到硬碟中。

Grace Hash Join

Conclusion​

對於一般的 join 來說，通常都會優先考慮 hash join，除非需要排序 (sort merge join) 或是 inner table 有 index (index nested loop join)。

Join Algorithms Comparison